1. 그래프와 인접행렬
기호로는 G(V, E)로 표시된다.
V(vortex) = 노드, 정점
E(edge) = 노드와 노드를 연결하는 간선
1. 무방향 그래프
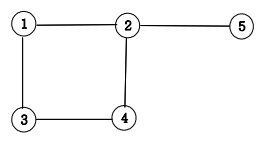
예시로 노드가 도시이고 간선이 도로일 경우가 된다.
1번 도시에서 2번 도시로 이동할 수 있고 2번 도시에서 1번 도시로 이동할 수 있다.
| a | b |
| 1 | 2 |
| 2 | 1 |
| 1 | 3 |
| 3 | 1 |
| 2 | 4 |
| 4 | 2 |
| 2 | 5 |
| 5 | 2 |
| 3 | 4 |
| 4 | 3 |
위의 그래프(인접행렬)를 표현하려면 2차 배열로 표현한다.
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 1 |
| 3 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 0 | 0 |
위 그래프는 무방향이기 때문에 아래와 같이 표현한다.
각 행과 열은 노드가 된다.
graph[a][b] = 1;
grahp[b][a] = 1;
2. 방향 그래프
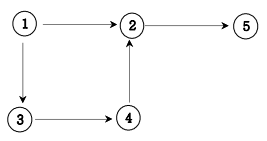
| a | b |
| 1 | 2 |
| 1 | 3 |
| 2 | 5 |
| 3 | 4 |
| 4 | 2 |
위의 그래프를 2차 배열로 표현해보자.
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 |
방향그래프이기 때문에 graph[a][b] = 1;로 표현된다.
3. 가중치 방향그래프

예를 들어 표현하자면, 1번 도시에서 2번 도시로 이동할 때 통행료가 2이다.
위의 그래프를 2차 배열로 표현해보자.
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 2 | 4 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 5 |
| 3 | 0 | 0 | 0 | 5 | 0 |
| 4 | 0 | 2 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 |
2. 문제 풀이
2 - 1. 경로 탐색(DFS-인접행렬: 노드개수가 적을 때)

방향그래프가 주어지면 1번 정점에서 N번 정점으로 가는 모든 경로의 가지 수를 출력하는 프 로그램을 작성하세요. 아래 그래프에서 1번 정점에서 5번 정점으로 가는 가지 수는
1 2 3 4 5
1 2 5
1 3 4 2 5
1 3 4 5
1 4 2 5
1 4 5
총 6 가지입니다.
*입력예제
5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5
*출력예제
6
아래와 같이 초기 설정을 해두고 시작한다.
function solution(n, arr) {
let answer=0;
let graph=Array.from(Array(n+1), () => Array(n+1).fill(0));
let ch=Array.from({ length: n+1 }, () => 0);
return answer;
}
let arr = [[1, 2], [1, 3], [1, 4], [2, 1], [2, 3], [2, 5], [3, 4], [4, 2], [4, 5]];
console.log(solution(5, arr)); // n은 노드 개수, arr은 간선 정보function solution(n, arr) {
let answer=0;
let graph=Array.from(Array(n+1), () => Array(n+1).fill(0));
let ch=Array.from({ length: n+1 }, () => 0);
for (let [a, b] of arr) {
graph[a][b] = 1;
}
function DFS(v) {
// 5까지 왔으면 1추가
if (v === n) answer++;
else {
for (let i = 1; i < n+1; i++) {
if (graph[v][i] === 1 && !ch[i]) {
// 돌아가지 못하게 걸어줘야한다.
ch[i] = 1;
DFS(i);
// 걸어준것을 풀어줘야한다.
ch[i] = 0;
}
}
}
}
ch[1] = 1;
DFS(1);
return answer;
}
let arr = [[1, 2], [1, 3], [1, 4], [2, 1], [2, 3], [2, 5], [3, 4], [4, 2], [4, 5]];
console.log(solution(5, arr));
2-2. 인접리스트
function solution(n, arr) {
let answer = 0;
let graph = Array.from({ length: n+1 }, () => Array());
let ch = Array.fron({ length: n+1 }, () => 0);
DFS(1)
return answer;
}
참고:
'알고리즘 풀이' 카테고리의 다른 글
| Node.js로 백준문제 테스트하기(with Replit) (0) | 2022.06.26 |
|---|---|
| BFS 넓이 우선 탐색 (0) | 2022.06.18 |
| DFS (0) | 2022.06.04 |
| Hash (0) | 2022.05.03 |
| [20211128]알고리즘 풀 (0) | 2021.11.28 |
